|
CGAL 6.1 - 2D Triangulations on Hyperbolic Surfaces
|
|
CGAL 6.1 - 2D Triangulations on Hyperbolic Surfaces
|
This package introduces a data structure and algorithms for triangulations of closed orientable hyperbolic surfaces. The triangulation is represented by an enriched CGAL::Combinatorial_map with complex number attributes on edges. Such a triangulation can be constructed from a surface given by a convex fundamental domain (see Section Fundamental Domains and Triangulations). A method is offered that randomly generates such domains for surfaces of genus two. On the other hand, the package works for any genus surface that may be provided by the user either as a fundamental domain or as an already computed triangulation. Functionalities are offered such as the Delaunay flip algorithm and the construction of a portion of the lift of the triangulation in the Poincaré disk model of the hyperbolic plane.
For the case of the Bolza surface, which is the most symmetric surface of genus two, we refer the user to the specific package 2D Periodic Hyperbolic Triangulations.
We assume some familiarity with basic notions from covering space theory and from the theory of hyperbolic surfaces. See for instance [2][3]. The Poincaré disk \( \mathbb{D} \) is a model of the hyperbolic plane whose point set is the open unit disk of the complex plane \( \mathbb{C} \). In this package, every hyperbolic surface \( S \) is closed (compact and without boundary) and orientable. The Poincaré disk \( \mathbb{D} \) is a universal covering space for \( S \), whose projection map \( \pi: \mathbb{D} \to S \) is a local isometry. For a point \( x \in S \), the infinite set \( \pi^{-1}(x) \) consists of lifts of \( x \), denoted \( \widetilde x \). This notion extends to paths and triangulations of S that can be lifted in \( \mathbb{D} \).
Let \( S \) be a hyperbolic surface. For representing \( S \), we cut it into topologically simple pieces. For a graph \( G \) embedded on \( S \), a face is a connected component of \( S \setminus G \). A graph \( G \) embedded on \( S \) defines a cellular decomposition of \( S \) if every face is a topological disk. In this document, every edge of a graph \( G \) embedded on \( S \) is a geodesic on \( S \). We consider two types of cellular decompositions of \( S \):
A decomposition of \( S \) that have only one face is a classical representation of the surface. Cutting \( S \) open along the edges of \( G \) results in a hyperbolic polygon \( P \) that is a fundamental domain for \( S \). Each edge of \( G \) is split into a pair of edges in \( P \). Every hyperbolic surface admits a fundamental domain \( P \) that is convex, meaning that the interior angles of \( P \) do not exceed \( \pi \).
A decomposition defined by the graph \( G \) is a triangulation of \( S \) if every face of \( G \) is a triangle: it is bounded by three edges of \( G \). Observe that this definition allows for triangulations with only one vertex. A triangulation of \( S \) can be obtained from a convex fundamental domain \( P \) of \( S \) by triangulating the interior of \( P \), and by gluing back the boundary edges that are paired in \( P \). The assumption that \( P \) is convex ensures that the interior of \( P \) can be triangulated naively by insertion of any maximal set of pairwise interior disjoint arcs of \( P \).
In order to perform fast and exact computations with a fundamental domain, every vertex must be a complex number whose type supports fast and exact computations. Under this constraint, it is still a research problem to generate domains of surfaces of genus greater than two. In genus two, this package generates fundamental domains whose vertices belong to \( \mathbb{Q} + i \mathbb{Q} \) (their real and imaginary parts are rational numbers). The exact generation process can be found in [5], together with a proof that the surfaces that can be generated in this way are dense in the space of hyperbolic surfaces genus two.
We represent every fundamental domain as a polygon in the Poincaré disk, given by the list of its vertices in counterclockwise order and by the list of its side pairings. This package can generate a random convex fundamental domain \( P \) of a surface of genus two, with eight vertices \( z_0, \dots, z_7 \in \mathbb{C} \). The vertices and the sides are in counterclockwise order, the side between \( z_0 \) and \( z_1 \) is \( A \), the side between \( z_4 \) and \( z_5 \) is \( \overline{A} \) and so on as on Figure 46.1. The side pairings are \( A \) with \(\overline{A} \) , \( B \) with \( \overline{B} \) , \( C \) with \( \overline{C} \) and \( D \) with \( \overline{D} \).
These octagons are symmetric, i.e. \( z_i = -z_{i+4} \) for every \( i \), where indices are modulo eight. Such octagons are described in [1].
Figure 46.1 Fundamental convex polygonal domain of a genus two surface.
Our representation is edge-based instead of the usual CGAL::TriangulationDataStructure_2 used for instance in the package 2D Periodic Hyperbolic Triangulations. This edge-based representation is more intrinsic to the surface and can handle non-simplicial triangulations, for instance a triangulation with only one vertex. We represent a triangulation \( T \) of a hyperbolic surface by an instance of CGAL::Combinatorial_map whose edges have complex number attributes that are cross ratios (defined shortly in the following). While the triangulation \( T \) is unambiguously determined by the combinatorial map and its cross ratios, the internal representation of \( T \) contains an additional data: the anchor, to be able to lift the triangulation in the Poincaré disk \( \mathbb{D} \). The anchor is a lift \( \widetilde t \) in \( \mathbb{D} \) of a triangle of \( T \). The anchor is represented by the three vertices \( \widetilde v_0, \widetilde v_1, \widetilde v_2 \) of \( \widetilde t \) in \( \mathbb{D} \), and by the dart in the combinatorial map of \( T \) corresponding to the oriented edge \( v_0v_1 \). A lift function is provided that computes a lift of each triangle of \( T \) in the Poincaré disk \( \mathbb{D} \), it starts from the anchor and then recursively constructs lifts of neighboring triangles using the cross ratios. See [5] for details.
The attribute of an edge \( e \) of \( T \) is the complex number \( R_T(e) \in \mathbb{C} \) called the cross ratio of \( e \) in \( T \), defined as follows. Consider the lift \( \widetilde T \) of \( T \) in the Poincaré disk \( \mathbb{D} \). In \( \widetilde T \), let \( \widetilde e \) be a lift of \( e \), see Figure 46.2. Orient \( \widetilde e \) arbitrarily, and let \( z_0 \in \mathbb{D} \) and \( z_2 \in \mathbb{D} \) be respectively the source and target vertices of \( \widetilde e \). In \( \widetilde T \), consider the triangle on the right of \( \widetilde e \), and let \( z_1 \in \mathbb{D} \) be the vertex distinct from \( z_0 \) and \( z_2 \) of this triangle. Similarly, consider the triangle on the left of \( \widetilde e \), and let \( z_3 \in \mathbb{D} \) be the vertex distinct from \( z_0 \) and \( z_2 \) of this triangle. Then \( R_T(e) = (z_3-z_1)(z_2-z_0) / ((z_3-z_0)(z_2-z_1)) \). This definition does not depend on the choice of the lift \( \widetilde e \), nor on the orientation of \( \widetilde e \). See [5] for details.
Figure 46.2 Computation of the cross ratio of an edge.
Let \( T \) be a triangulation of a hyperbolic surface. An edge \( e \) of \( T \) satisfies the Delaunay criterion if the imaginary part of its cross ratio \(R_T(e)\) is non-positive. This definition is equivalent to the usual formulation for the triangulation lifted in \( \mathbb{D} \): there exists a disk containing \( \widetilde e \) and that does not contain any other vertices of \( \widetilde T \) in its interior. Then \( T \) is a Delaunay triangulation if every edge of \( T \) satisfies the Delaunay criterion. If an edge \(e \) of \( T \) does not satisfy the Delaunay criterion, then \(e \) is called Delaunay flippable, and then the two triangles incident to \( e \) form a strictly convex quadrilateral, so \( e \) can be deleted from \( T \) and replaced by the other diagonal of the quadrilateral. This operation is called a Delaunay flip. When a flip occurs, the cross ratios of the involved edges are modified via simple formulas. The Delaunay flip algorithm flips edges that do not satisfy the Delaunay until no more edges violate the criterion, with no preference on the order of the flips. This algorithm terminates, and outputs a Delaunay triangulation of \( S \) [4].
The concept ComplexNumber describes a complex number type modeled by CGAL::Complex_number. Complex numbers are used to encode the cross ratios, for the coefficients of isometries and implicitly to work with points in the Poincaré disk. Most classes of the package are templated by the concept HyperbolicSurfaceTraits_2. It is a refinement of HyperbolicDelaunayTriangulationTraits_2 and is modeled by CGAL::Hyperbolic_surface_traits_2. It defines the geometric objects (points, segments...) forming the lifted triangulation in the Poincaré disk.
The package offers three main classes:
CGAL::Triangulation_on_hyperbolic_surface_2 represents a triangulation of a hyperbolic surface. It offers functions for the generation of the triangulation from a convex fundamental domain, the Delaunay flip algorithm and the construction of a portion of the lift of the triangulation in the Poincaré disk.CGAL::Hyperbolic_fundamental_domain_2 represents a convex fundamental domain of a hyperbolic surface.CGAL::Hyperbolic_fundamental_domain_factory_2 generates random convex fundamental domains of surfaces of genus two.The secondary class CGAL::Hyperbolic_isometry_2 defines isometries in the Poincaré disk together with operations to work with them.
The function CGAL::Triangulation_on_hyperbolic_surface_2::lift() computes the lift of each triangle in the hyperbolic plane, enabling its visualization (see Figure 46.3). This package contains a demo (found in the folder Triangulation_on_hyperbolic_surface_2/demo), which can be used to display triangulations.
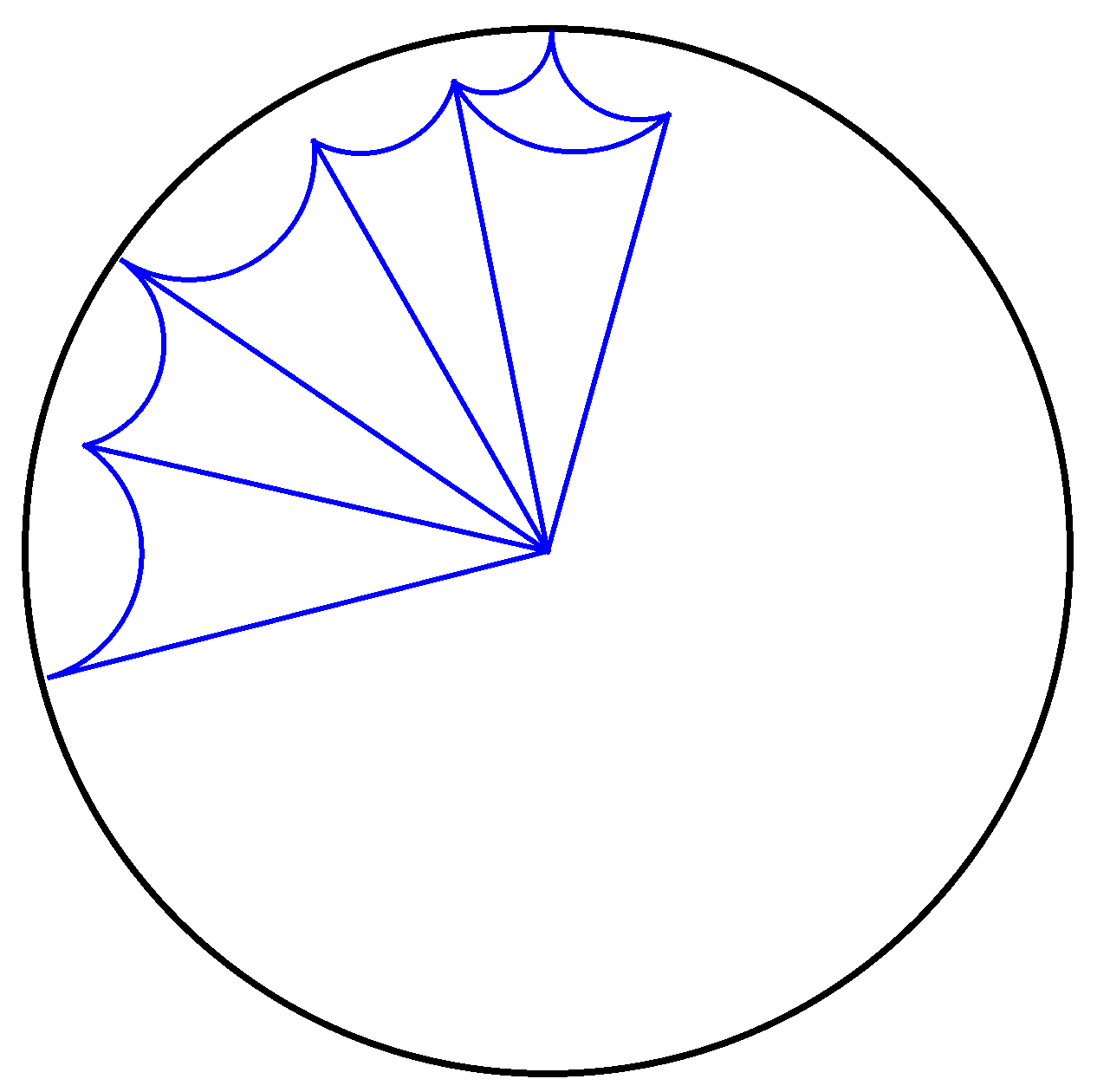
Figure 46.3 Lift, in the Poincaré disk, of a Delaunay triangulation of a genus two hyperbolic surface with one vertex.
The example below generates a convex fundamental domain of a surface of genus two, triangulates the domain, applies the Delaunay flip algorithm to the resulting triangulation, saves and prints the Delaunay triangulation.
File Triangulation_on_hyperbolic_surface_2/Triangulation_on_hyperbolic_surface_2.cpp
This package implements the Delaunay flip algorithm described in the hyperbolic setting by Vincent Despré, Jean-Marc Schlenker and Monique Teillaud in [4] using the data structure for representing triangulations presented in [5]). It also implements the generation of domains described by Vincent Despré, Loïc Dubois, Benedikt Kolbe and Monique Teillaud in [5], based on results of Aline Aigon-Dupuy, Peter Buser, Michel Cibils, Alfred F Künzle and Frank Steiner [1]. The code and the documentation of the package were written by Loïc Dubois, under regular discussions with Vincent Despré, Marc Pouget and Monique Teillaud. The authors acknowledge support from the grants SoS and MIN-MAX of the French National Research Agency ANR.