|
CGAL 6.1 - 3D Constrained Triangulations
|
|
CGAL 6.1 - 3D Constrained Triangulations
|
3D triangulations partition space and are useful in many applications. In some cases, it is important to ensure that specific faces, such as those representing the sharp features of an object, appear in the output. When a triangulation exactly respects these constraints, it is called a constrained triangulation. However, it is sometimes only possible to preserve the geometry of the constraints, but not their exact combinatorics. In such cases, additional points, called Steiner points, must be inserted. This process results in a conforming triangulation.
This package implements an algorithm for constructing conforming triangulations of 3D polygonal constraints. Specifically, it requires that these piecewise linear constraints are provided as a piecewise linear complex (PLC). The resulting triangulations are of type Triangulation_3, as described in the chapter 3D Triangulations.
The article by Cohen-Steiner et al. [2] discusses the problem of constructing conforming Delaunay triangulations and proposes an algorithm to address it. Si et al.'s work [7], [8], [4], presents an algorithm for computing conforming constrained Delaunay triangulations in 3D.
This section introduces the key concepts necessary to understand and use this package effectively.
A piecewise linear complex (PLC) is the three-dimensional generalization of a planar straight-line graph. It consists of a finite set of vertices, edges, and polygonal faces that satisfy the following properties:
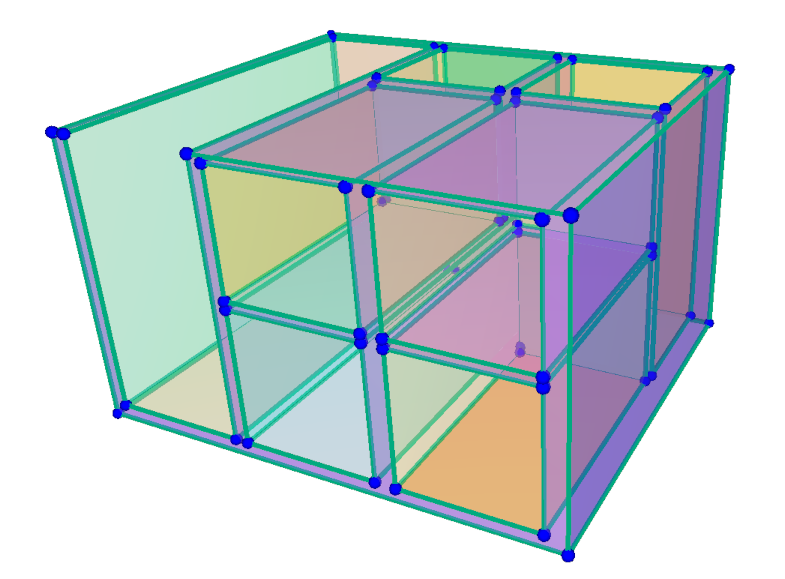
Figure 50.2 A piecewise linear complex, composed of planar faces connected by edges and vertices.
The algorithms developed in this package are designed to compute a constrained Delaunay triangulation that contains a given set of polygonal constraints in 3D as a subcomplex.
A triangulation is a Delaunay triangulation if the circumscribing sphere of any simplex in the triangulation contains no vertex in its interior (see chapter 3D Triangulations for more details on Delaunay triangulations).
A constrained Delaunay triangulation of a PLC is a constrained triangulation that is as close as possible to being Delaunay, given that some faces are marked as constrained. More precisely, a triangulation is constrained Delaunay if, for any simplex \(s\) of the triangulation, the interior of its circumscribing sphere contains no vertex of the triangulation that is visible from any point in the interior of the simplex \(s\). Two points are visible if the open line segment joining them does not intersect any polygonal face of the PLC, except for polygonal faces that are coplanar with the segment.
In 3D, constrained triangulations do not always exist. This can be demonstrated using the example of Schönhardt polyhedra [5] (see Figure 50.3), [1]. Shewchuk [6] demonstrated that for any PLC, there exists a refined version of the original PLC that admits a constrained Delaunay triangulation. This refinement is achieved by adding Steiner vertices to the input edges and polygonal faces. The constrained triangulation built on this refined PLC is known as a conforming constrained Delaunay triangulation (CCDT for short). Figure 50.4 illustrates an example of a conforming constrained Delaunay triangulation constructed from a PLC.

Figure 50.3 A Schönhardt polyhedron.

Figure 50.4 Left: PLC (360 vertices); Right: CCDT (2452 vertices).
The algorithm implemented in this package is based on the work of Hang Si et al., who developed particular algorithms for constructing conforming constrained Delaunay triangulations from PLCs. The corresponding implementation is designed to handle points whose coordinates are floating-point numbers. [7], [8], [4].
There is no universal or canonical way to represent all possible PLCs in CGAL.
Any polyhedral surface is a PLC, so any model of FaceListGraph, such as CGAL::Surface_mesh, can be used to represent such a PLC. In this representation, the geometric structure of the PLC is directly mapped to the elements of the CGAL::Surface_mesh:
A PLC can also be represented as a polygon soup: a collection of vertices and a set of polygons, where each polygon is defined by an ordered list of vertices, without explicit connectivity information between polygons. For a polygon soup to represent a valid PLC, its polygons must satisfy the polygonal faces properties described in the previous section. This approach allows for the representation of non-manifold geometries; however, polygons in a polygon soup cannot have holes.
This package also provides a way to group polygonal faces into distinct surface patches using a property map, named plc_face_id. Each polygon can be assigned a patch identifier, allowing multiple polygonal faces to form a continuous surface patch, which may include holes. Some necessary conditions must be satisfied for these patches to be used in the conforming constrained Delaunay triangulation construction:
When this property map is provided, the input PLC is interpreted in terms of its polygonal faces, edges and vertices as follows:
This package provides a primary class, CGAL::Conforming_constrained_Delaunay_triangulation_3. This class is templated by a geometric traits class and an underlying triangulation class, allowing for flexibility and customization.
In addition to the main class, the package includes several auxiliary classes that define the types of vertices, cells, and associated metadata used within the triangulation. These supporting classes enable users to extend or adapt the triangulation data structure to their specific needs.
Two overloads of the constructor function CGAL::make_conforming_constrained_Delaunay_triangulation_3() are provided to facilitate the creation of a CGAL::Conforming_constrained_Delaunay_triangulation_3 object from either a surface mesh or a polygon soup.
The requirements for geometric objects and operations are specified by the traits class concept ConformingConstrainedDelaunayTriangulationTraits_3. Any CGAL kernel is a model of this concept. However, because this package builds upon the 3D Triangulation package, it inherits the requirement that the traits class must provide exact predicates.
A key aspect of this algorithm is the creation of new points, known as Steiner points, which are inserted on the segments and polygons forming the input PLC polygonal faces. If a traits class with inexact constructions is used, it cannot be guaranteed that these points will lie exactly on the intended segments or polygons. As a result, the output will only approximate the input, with the accuracy limited by the rounding of the computed Steiner points.
Furthermore, when using inexact constructions, the algorithm may fail if the input PLC contains non-adjacent simplices that are too close to each other. In such cases, the triangulation process will emit an error if the distance between simplices falls below an internally computed threshold. An error message describing the involved simplices will be displayed on the standard output. If the issue is caused by poorly shaped triangles, functions such as CGAL::Polygon_mesh_processing::remove_almost_degenerate_faces() may help resolve the problem.
The following example illustrates how to use the helper function CGAL::make_conforming_constrained_Delaunay_triangulation_3() to construct a conforming constrained Delaunay triangulation from a given PLC.
The triangulation is saved in the MEDIT file format, using the CGAL::IO::write_MEDIT() function.
File Constrained_triangulation_3/conforming_constrained_Delaunay_triangulation_3.cpp
You can also construct a conforming constrained Delaunay triangulation from a polygon soup. The following example demonstrates how to create such a triangulation from a collection of polygons without explicit connectivity information.
File Constrained_triangulation_3/ccdt_3_from_soup.cpp
If the user already knows the set of polygonal face identifiers to associate with each PLC face, this information can be provided and preserved throughout the construction of the conforming constrained Delaunay triangulation.
The following example demonstrates how to detect planar surface patches and remesh them as coarsely as possible using CGAL::Polygon_mesh_processing::remesh_planar_patches() from the Polygon Mesh Processing package. The resulting patches and segmentation are then used to build a conforming constrained Delaunay triangulation.
When the named parameter plc_face_id is specified, each constrained facet in the 3D triangulation is assigned to the corresponding input PLC face, as identified by the provided property map. If this parameter is not specified, each input polygonal face is assigned a unique face index.
Figure Figure 50.5 shows the benefit of using the plc_face_id property map. On the last line of the figure, the input PLC is enriched with a segmentation of the planar faces, provided via the plc_face_id property map. In the resulting conforming constrained Delaunay triangulation, only the boundary edges of the PLC faces are constrained, while the other edges never get inserted as edges of the 3D triangulation.
Without the plc_face_id property map, all edges of the PLC faces are constrained, each PLC face is considered as a constraint, possibly resulting in a 3D triangulation with surfaces that are more refined than necessary.
File Constrained_triangulation_3/conforming_constrained_Delaunay_triangulation_3_fimap.cpp
Figure 50.5 shows the input and output of this triangulation construction example.
If the user does not know the set of polygonal face identifiers to associate with each PLC face, this information can be automatically detected using the CGAL::Polygon_mesh_processing::region_growing_of_planes_on_faces() function from the Polygon Mesh Processing package.
The following example demonstrates how to detect planar surface patches and build a conforming constrained Delaunay triangulation using the detected segmentation. The named parameter plc_face_id is used to associate each facet of the triangulation with the corresponding input PLC face.
File Constrained_triangulation_3/ccdt_3_fimap_region_growing.cpp
Given a PLC, the algorithms in this package can construct a conforming constrained Delaunay triangulation, provided the input surface can be represented as a valid surface mesh or a collection of surface meshes, and does not contain self-intersections. Several preprocessing functions are available in the Polygon Mesh Processing package to help ensure these preconditions are met.
The following example demonstrates how to construct a conforming constrained Delaunay triangulation from an input mesh that is not triangulated and may contain self-intersections, using autorefinement.
File Constrained_triangulation_3/ccdt_3_after_autorefinement.cpp
The function CGAL::Polygon_mesh_processing::does_self_intersect() is used to detect self-intersections, but it requires the input mesh to be triangulated. Therefore, the input mesh must first be triangulated using CGAL::Polygon_mesh_processing::triangulate_faces() before performing the self-intersection check.
If self-intersections are found, the triangulated mesh is converted into a triangle soup, which is then processed with CGAL::Polygon_mesh_processing::autorefine_triangle_soup() to resolve the self-intersections.
After constructing the triangulation, you can improve its quality or adapt it to a specific sizing field by applying the CGAL::tetrahedral_isotropic_remeshing() function from the Tetrahedral Remeshing package.
The following example demonstrates how to remesh a conforming constrained Delaunay triangulation.
File Constrained_triangulation_3/remesh_constrained_Delaunay_triangulation_3.cpp
The following table of figures (Figure 50.5) illustrates some results of the examples provided in this package. The left column shows the input PLC, while the right column displays the resulting conforming constrained Delaunay triangulation.
From top to bottom, the lines show different input PLC, from the same input triangulated surface and, for each of them, the resulting conforming constrained Delaunay triangulation. The input data are:
CGAL::Polygon_mesh_processing::region_growing_of_planes_on_faces() as done in example Build a Conforming Constrained Delaunay Triangulation with Detected Polygon Identifiers; CGAL::Polygon_mesh_processing::remesh_planar_patches() as in example Build a Conforming Constrained Delaunay Triangulation with Known Polygon Identifiers; CGAL::Polygon_mesh_processing::region_growing_of_planes_on_faces() as in example Build a Conforming Constrained Delaunay Triangulation with Detected Polygon Identifiers. On the fourth line, the input PLC is remeshed using CGAL::Polygon_mesh_processing::isotropic_remeshing(). The resulting conforming constrained Delaunay triangulation contains fewer vertices than the input remeshed and segmented input PLC. This reduction occurs because only the boundary edges of the PLC faces are marked as constraints in the triangulation; interior edges that do not lie on the boundaries of surface patches (as defined by plc_face_id) are ignored. As a result, these non-boundary edges are omitted from the triangulation, leading to a coarser triangulation.

Figure 50.5 A collection of conforming constrained Delaunay triangulations built from different inputs. The left column shows the input PLC, while the right column displays the resulting 3D triangulation.
The initial version of this package was implemented by Laurent Rineau and released in CGAL 6.1 (2025). Jane Tournois contributed to the documentation and helped improve the API. The package design and algorithms are grounded in the theoretical work of Hang Si et al. on meshing algorithms [7], [4].